오늘의 TIL - 트리 정리 참고-엔지니어 대한민국님 유투브

Tree

부모 - 자식을 가지는 계층 구조.

각 노드가 하나 이상의 자식 노드를 가진다.
더 이상 자식이 없으면 leaf 라고 부른다.
child 가 2개 까지만 붙는 tree 를 binary tree 라고 한다.

binary tree & binary search tree (이진 검색 트리)

binary tree

다른 조건 없이 각 노드에 최대 2개까지의 자식 노드 있음.

binary search tree

왼쪽 노드와 그 이하 자식 노드들은 현재 노드보다 작음
오른쪽 노드와 그 이하 자식들은 현재 노드보다 큼. 어떤 값을 찾을때 유용하게 쓸 수 있다.

balanced - unbalanced

왼쪽 오른쪽 노드 개수가 너무 차이나지 않으면 balanced 임.
balanced 예시 : AVL tree

complete binary tree

모든 노드들이 레벨 별로 왼쪽부터 채워져있는 이진 트리

full binary tree

자식 노드를 가지려면 최대 2개를 다 채워서 가지고, 아니면 가지지 않는 것

perfect binary tree

모든 노드들이 왼쪽부터 채워져있으며 2개의 자식노드를 다 채운 트리
완벽한 피라미드 구조를 띄고 있다 .

binary tree 의 탐색법

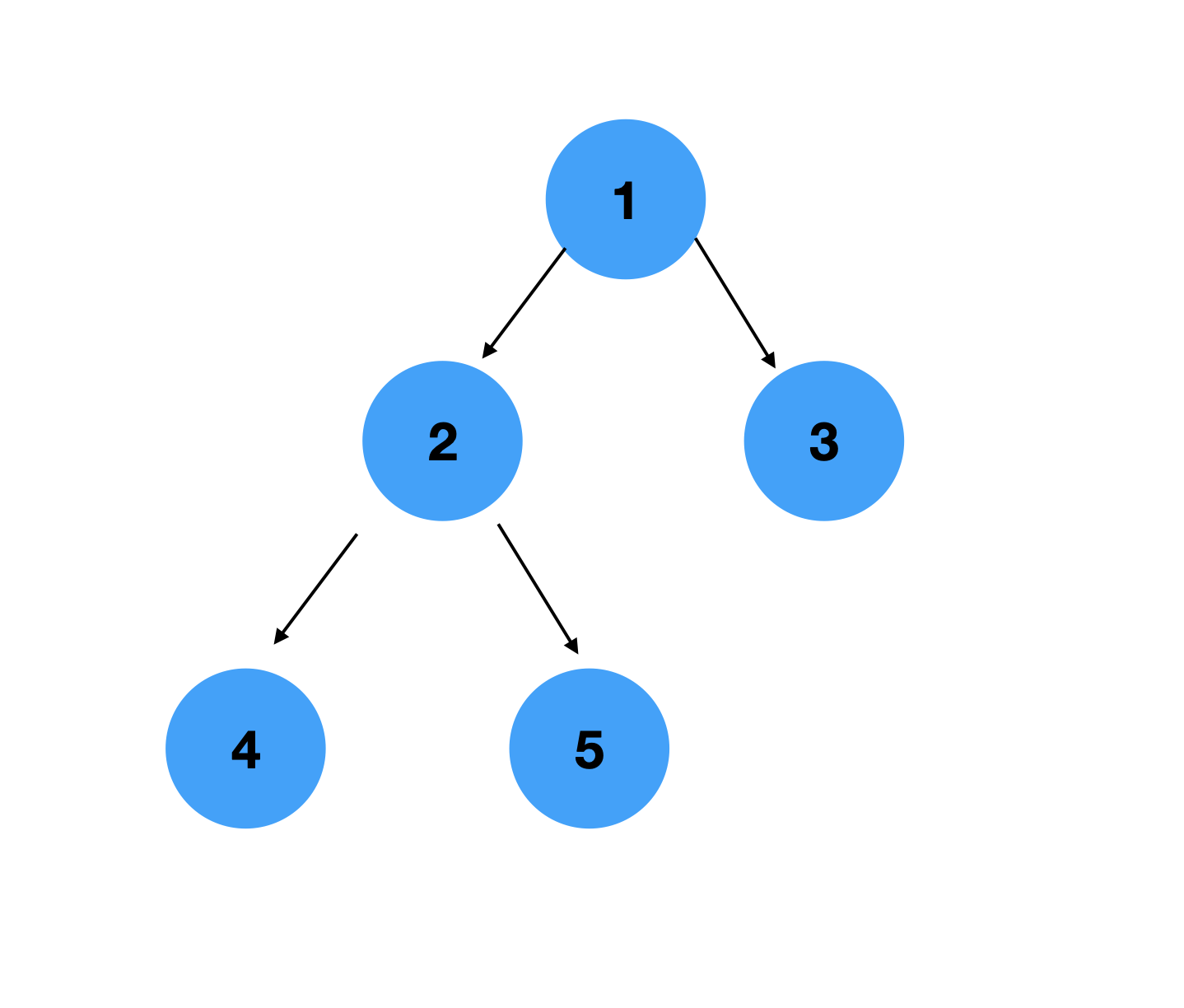이 그림으로 설명하겠다.

Inorder

left -> root -> right 의 순으로 탐색.
루트 노드인 1 부터 탐색한다고 하면, 더이상 왼쪽 아래 자식 노드가 없을 때까지 왼쪽으로 내려간다. 거기서부터 탐색 시작한다.
4 -> 2 -> 5 -> 1 -> 3

Preorder

root -> left -> right 순 위에서부터 루트 (본인) 부터 찾고 왼쪽 노드부터 탐색한다.
1 -> 2 -> 4 -> 5 -> 3

Postorder

left -> right -> root 순
루트 노드인 1 부터 탐색한다고 하면, 더이상 왼쪽 아래 자식 노드가 없을 때까지 왼쪽으로 내려가되 같은 레벨부터 본다.
4 -> 5 -> 2 -> 3 -> 1

binart tree 탐색법 세가지 java 구현

트리 테스트라는 트리 구조를 저장할 클래스를 만들었다.
각 노드는 본인의 값과 왼쪽, 오른쪽 아래 자식 노드를 가지고 있다. 재귀 호출로 구현한다. (아래 노드들로 계속 내려갈 수 있도록)

  
public class TreeTest {
    public class Node{
        int data;
        Node left;
        Node right;
    }

    Node root;

    public Node getRoot(){
        return root;
    }

    public void setRoot(Node firstNode){
        root = firstNode;
    }

    public Node makeNode(int data, Node left, Node right){
        Node newNode = new Node();
        newNode.data = data;
        newNode.left = left;
        newNode.right=right;
        return newNode;
    }

    public void inOrder(Node node){
        if(node !=null){  
            inOrder(node.left);
            System.out.println(node.data);
            inOrder(node.right);
        }
    }

    public void preOrder(Node node){
        if(node !=null){
            System.out.println(node.data);
            preOrder(node.left);
            preOrder(node.right);
        }
    }

    public void postOrder(Node node){
        if(node !=null){
            postOrder(node.left);
            postOrder(node.right);
            System.out.println(node.data);
        }
    }
}

테스트 하기 위해서는 자료 구조를 아래 노드부터 채우고 루트 노드에서 탐색법을 검증해본다.

  
public class TestForTree {
    TreeTest tree;

    @BeforeEach
    void init(){
        tree =new TreeTest();
        TreeTest.Node node4 = tree.makeNode(4,null,null);
        TreeTest.Node node5 = tree.makeNode(5,null,null);
        TreeTest.Node node2 = tree.makeNode(2,node4,node5);
        TreeTest.Node node3 = tree.makeNode(3,null,null);
        TreeTest.Node root = tree.makeNode(1,node2,node3);
        tree.setRoot(root);
    }

    @Test
    @DisplayName("inOrder 4 2 5 1 3")
    void inOrderTest(){
        tree.inOrder(tree.getRoot());
    }

    @Test
    @DisplayName("preOrder 1 2 4 5 3")
    void preOrderTest(){
        tree.preOrder(tree.getRoot());
    }

    @Test
    @DisplayName("postOrder 4 5 2 3 1")
    void postOrderTest(){
        tree.postOrder(tree.getRoot());
    }

자료구조 다시보기- tree